Box2D C++ tutorials - Rotating to a given angle
Last edited: July 14 2013
Chinese version ->
中文
Rotating a body to a given angle
This topic is similar to the previous topic but deals with rotating a body instead
of linear movement. Rotating a body can be also done by setting the angle directly or
by using torque/impulse methods, with the same point to note that setting
the angle directly means the body is not participating correctly in the physics
simulation.
To experiment with these all we need is one dynamic body, and it would be nice if there was
no gravity so it stays on the screen for us. We will need to give the body a fixture which
has a distinct direction, so we can check if it's facing the right way. Let's set it up as
a polygon with one 'pointy' vertex:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| //class member variable
b2Body* body;
FooTest() {
//body definition
b2BodyDef myBodyDef;
myBodyDef.type = b2_dynamicBody;
//hexagonal shape definition
b2PolygonShape polygonShape;
b2Vec2 vertices[6];
for (int i = 0; i < 6; i++) {
float angle = -i/6.0 * 360 * DEGTORAD;
vertices[i].Set(sinf(angle), cosf(angle));
}
vertices[0].Set( 0, 4 ); //change one vertex to be pointy
polygonShape.Set(vertices, 6);
//fixture definition
b2FixtureDef myFixtureDef;
myFixtureDef.shape = &polygonShape;
myFixtureDef.density = 1;
//create dynamic body
myBodyDef.position.Set(0, 10);
body = m_world->CreateBody(&myBodyDef);
body->CreateFixture(&myFixtureDef);
//zero gravity
m_world->SetGravity( b2Vec2(0,0) );
} |

To set a point for this body to rotate towards, we'll use the mouse input function:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| //class member variable
b2Vec2 clickedPoint;
//in class constructor
clickedPoint = b2Vec2(0,20);//initial starting point
//override parent class
void MouseDown(const b2Vec2& p)
{
//store last mouse-down position
clickedPoint = p;
//do normal behaviour
Test::MouseDown( p );
}
//inside Step()
glPointSize(4);
glBegin(GL_POINTS);
glVertex2f( clickedPoint.x, clickedPoint.y );
glEnd(); |
Don't worry if you don't recognize the code in the Step() function, this is just to draw
the location of clickedPoint on the screen.
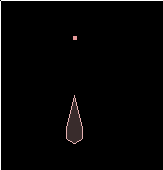
This point will move to wherever the mouse was last clicked. It still does the default
behaviour of grabbing objects in the scene too, so it's a little strange but good enough
for what we need.
Setting angle directly
This is as simple as using SetTransform to set the angle, but first we need to know
what the angle should be, given the location of the body and the location of the target
point. Add this to the Step() function to do it every time step:
1
2
3
4
5
6
7
8
9
10
| //in Step() function
float bodyAngle = body->GetAngle();
b2Vec2 toTarget = clickedPoint - body->GetPosition();
float desiredAngle = atan2f( -toTarget.x, toTarget.y );
//view these in real time
m_debugDraw.DrawString(5, m_textLine, "Body angle %.3f", bodyAngle * RADTODEG);
m_textLine += 15;
m_debugDraw.DrawString(5, m_textLine, "Target angle %.3f", desiredAngle * RADTODEG);
m_textLine += 15; |
Now click around the screen to see how the result changes depending
on the angle between the body to the target point. Notice that if the body
keeps spinning in one direction, its angle gets larger in that direction and can
exceed 360 degrees, but the target angle we calculate is only ever between -180 and 180.
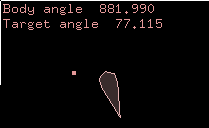
Now that we've seen how the angle calculation behaves, try the SetTransform method
to align the body, and you should see the body align itself instantly to face at the target point.
1
| body->SetTransform( body->GetPosition(), desiredAngle ); |

Try throwing the body so that it moves very slowly close by the target point, and you
may see a side effect caused by this method not simulating physics realistically.
I found that the body can either be pushed away from the target point, or go into
an orbit around it. This is because for this body the center of mass is offset a little,
and also I think because the angular velocity from the previous time step becomes
invalid when we directly set the angle. In any case, it's worth noting that by setting
the angular velocity to zero to eliminate the effects of the angular velocity from
the previous time step, the problem goes away:
1
| body->SetAngularVelocity(0); |
To make the body turn gradually, just limit the change in angle for each time step:
1
2
3
4
| float totalRotation = desiredAngle - bodyAngle;
float change = 1 * DEGTORAD; //allow 1 degree rotation per time step
float newAngle = bodyAngle + min( change, max(-change, totalRotation));
body->SetTransform( body->GetPosition(), newAngle ); |
Have you noticed something odd when the target position is below the body? Angles on
the left are positive values, and angles on the right are negative, spanning from -180 to 180.
This means that when the target crosses directly below the body, the desired angle
can jump from say, 179 to -179 which causes the body to do almost a full rotation (358 degrees) even though
the target was only 2 degrees away! We could fix this by noting that the body should
never need to rotate more than 180 degrees to face the right direction. Whenever
totalRotation exceeds 180 degress we can adjust it like:
1
2
| while ( totalRotation < -180 * DEGTORAD ) totalRotation += 360 * DEGTORAD;
while ( totalRotation > 180 * DEGTORAD ) totalRotation -= 360 * DEGTORAD; |
This will also take care of the fact that the body's angle can be a very high value
if it has rotated the same way many times.
Using torques
For a more physically realistic method, a torque can be applied to turn the body: We could try this to start with:
1
2
3
4
| float totalRotation = desiredAngle - bodyAngle;
while ( totalRotation < -180 * DEGTORAD ) totalRotation += 360 * DEGTORAD;
while ( totalRotation > 180 * DEGTORAD ) totalRotation -= 360 * DEGTORAD;
body->ApplyTorque( totalRotation < 0 ? -10 : 10 ); |
Hmm... doesn't really work does it? The problem with this method is that the force
is applied right up until the body is facing the right direction, which might sound
ok but it means the body picks up angular momentum so that it swings right past the
target point and then needs to be pushed back, and so on, forever. What we need to
do is apply less force as the body gets closer to the correct angle... but simply
scaling the force down relative to the remaining angle will not fix the problem either - try it.
Since the problem is caused by the current angular velocity affecting future time steps,
we need to take that into account. We can calculate the angle of the body in the next
time step without applying any torque - this is what would happen if we just left it alone -
and use that in place of the current angle (with the default testbed framerate of 60Hz):
1
2
3
| float nextAngle = bodyAngle + body->GetAngularVelocity() / 60.0;
float totalRotation = desiredAngle - nextAngle;//use angle in next time step
body->ApplyTorque( totalRotation < 0 ? -10 : 10 ); |
While that looks almost the same as before, if you wait a bit you'll see that at least
it eventually stops in the right place instead of swinging about forever. While technically
that completes this scenario, the slow convergence is probably not satisfactory for most applications.
The solution is to look ahead more than one time step to adjust the rate at which
the correct angle is reached. I found that looking ahead about 1/3 second gave a result
like a magnetic compass needle:
1
| float nextAngle = bodyAngle + body->GetAngularVelocity() / 3.0;// 1/3 second |
How about an intantaneous spin? As in the previous topic, we could try a very large force
for one time step, along with the 'looking ahead' idea above. The equation to find the
torque to apply is the same as the linear version but uses angular velocity and angular mass.
Angular mass is known as rotational inertia, commonly denoted as I.
Using the formula T = Iv/t where
T is the torque we want to know, I is the rotational inertia of the body, v is the rotational
velocity and t is the time we will apply the torque, as before:
1
2
3
4
5
6
7
| float nextAngle = bodyAngle + body->GetAngularVelocity() / 60.0;
float totalRotation = desiredAngle - nextAngle;
while ( totalRotation < -180 * DEGTORAD ) totalRotation += 360 * DEGTORAD;
while ( totalRotation > 180 * DEGTORAD ) totalRotation -= 360 * DEGTORAD;
float desiredAngularVelocity = totalRotation * 60;
float torque = body->GetInertia() * desiredAngularVelocity / (1/60.0);
body->ApplyTorque( torque ); |
Note that this is not quite instantaneous, but it usually gets the body in the right
rotation within 2-3 time steps which is usually good enough for practical purposes.
Update: this will not work correctly for bodies with
a center of mass that is not on their origin, like the one we have here :( Currently the
Box2D API only allows access to the inertia about the body origin, whereas we are applying
a torque about the center of mass. I am hoping future releases of the API will make the
inertia about the center of mass available.
Using impulses
As in the last topic, instantaneous movement using impulses is the same as the above
code, but without the time factor:
1
2
3
4
5
6
7
| float nextAngle = bodyAngle + body->GetAngularVelocity() / 60.0;
float totalRotation = desiredAngle - nextAngle;
while ( totalRotation < -180 * DEGTORAD ) totalRotation += 360 * DEGTORAD;
while ( totalRotation > 180 * DEGTORAD ) totalRotation -= 360 * DEGTORAD;
float desiredAngularVelocity = totalRotation * 60;
float impulse = body->GetInertia() * desiredAngularVelocity;// disregard time factor
body->ApplyAngularImpulse( impulse ); |
And for a gradual change, just limit the change in rotation allowed per time step:
1
2
3
4
5
6
7
8
9
| float nextAngle = bodyAngle + body->GetAngularVelocity() / 60.0;
float totalRotation = desiredAngle - nextAngle;
while ( totalRotation < -180 * DEGTORAD ) totalRotation += 360 * DEGTORAD;
while ( totalRotation > 180 * DEGTORAD ) totalRotation -= 360 * DEGTORAD;
float desiredAngularVelocity = totalRotation * 60;
float change = 1 * DEGTORAD; //allow 1 degree rotation per time step
desiredAngularVelocity = min( change, max(-change, desiredAngularVelocity));
float impulse = body->GetInertia() * desiredAngularVelocity;
body->ApplyAngularImpulse( impulse ); |
Once again the swinging problem can be controlled by how far ahead the nextAngle
variable looks.
 To set a point for this body to rotate towards, we'll use the mouse input function:
To set a point for this body to rotate towards, we'll use the mouse input function:
 This point will move to wherever the mouse was last clicked. It still does the default
behaviour of grabbing objects in the scene too, so it's a little strange but good enough
for what we need.
This point will move to wherever the mouse was last clicked. It still does the default
behaviour of grabbing objects in the scene too, so it's a little strange but good enough
for what we need. Now that we've seen how the angle calculation behaves, try the SetTransform method
to align the body, and you should see the body align itself instantly to face at the target point.
Now that we've seen how the angle calculation behaves, try the SetTransform method
to align the body, and you should see the body align itself instantly to face at the target point.
 Try throwing the body so that it moves very slowly close by the target point, and you
may see a side effect caused by this method not simulating physics realistically.
I found that the body can either be pushed away from the target point, or go into
an orbit around it. This is because for this body the center of mass is offset a little,
and also I think because the angular velocity from the previous time step becomes
invalid when we directly set the angle. In any case, it's worth noting that by setting
the angular velocity to zero to eliminate the effects of the angular velocity from
the previous time step, the problem goes away:
Try throwing the body so that it moves very slowly close by the target point, and you
may see a side effect caused by this method not simulating physics realistically.
I found that the body can either be pushed away from the target point, or go into
an orbit around it. This is because for this body the center of mass is offset a little,
and also I think because the angular velocity from the previous time step becomes
invalid when we directly set the angle. In any case, it's worth noting that by setting
the angular velocity to zero to eliminate the effects of the angular velocity from
the previous time step, the problem goes away:


