Box2D C++ tutorials - Projected trajectories
Last edited: April 15 2014Projected trajectory
Halt! You should have a good understanding of
the basic tutorials before venturing further.
Here's another question which comes up quite frequently regarding projectile motion in Box2D - "When a body is thrown or launched in the air, how can I tell...
- what path it will follow?
- the maximum height it will reach?
- how fast to launch it to reach a desired height?
- what it will hit?
- how it will bounce?
There are two ways this information can be found. One is to use a basic projectile motion formula and plug in the variables you know to find the one you don't. The other way is to fully simulate the motion of the object by running the Box2D world step to see how it will move. This topic will cover the first of these methods. Let's first take a quick look at the pros and cons of both the 'plugin formula' and the 'fully simulated world' methods.
The advantage of the plugin formula method is obviously that it requires less processing time, and is much easier to set up because there is no tricky management of world state required. The disadvantage is that if there are other dynamic objects in the world, the plugin formula method cannot actually answer the last two of the questions above: what will it hit and how will it bounce. Since we are looking into the future, in order to know what the projectile will hit we would also need to know the future positions of all the other things moving around in the scene too.
On the other hand, the fully simulated world method can answer all of the questions above because it does know the future positions of all the other objects in the scene... but this information comes at a cost. Firstly it could be quite a processing intensive task - as the user moves the projected trajectory around, the mouse move updates (or whatever input is being used) could be generated dozens of times per second. If you want show a projected trajectory for the next one second at 60fps this would mean you need to copy the entire world state and step it forwards 60 times, for every mouse movement. If your world is not too complex this is probably still fine, but there is also the extra work involved in making a copy of the world to use for this stepping forwards. This would require some kind of serialization process to go through the current world and make a duplicate of all the bodies and fixtures into a new temporary world (if you are interested in this method you may find the b2djson loader helpful) but due to Box2D's warm starting optimizations there is no guarantee that the copied world and the original will behave exactly the same. Finally, this method does not give you a direct formulaic answer to questions 2 and 3 above - for example if you want to know the maximum height reached, or how high the projectile will be at time x, you have to run all the world steps up to that point in order to find out.
So that is the reasoning for going with the plugin formula method for this topic. Just remember that if you really do need full knowledge of how the projectile will interact with other dynamic objects, you will need to use the fully simulated world approach. But in most cases I'm guessing it's enough to show the user a predicted path or let the 'AI' do something sensible.
One more thing before we get started - you cannot predict anything if you are using a variable length time step. To use the plugin formula method to make predictions about the trajectory you will need to be using the same time step size for every step. Yeah that should go without saying but I said it anyway.
The formula
To make a long story short, the formula we'll use to find a point at a given time along the trajectory path is as follows. (Click here if you're interested in the long story.)
Velocity measured as distance moved per timestep
Acceleration measured as change in velocity per timestep
h = starting height
v = starting velocity
a = acceleration (gravity, constant)
Height changes by current velocity every time step
Velocity changes by constant acceleration every time step
Height Velocity
h0 = h v0 = v + a <- engine applies gravity before moving!
h1 = h0 + v0 v1 = v0 + a
h2 = h1 + v1 v2 = v1 + a
h3 = h2 + v2 v3 = v2 + a
h4 = h3 + v3 v4 = v3 + a
Expanded velocity
v0 = v + a
v1 = v + a + a
v2 = v + a + a + a
v3 = v + a + a + a + a
Expanded height
h0 = h
h1 = h + v + a
h2 = h + v + a + v + a + a
h3 = h + v + a + v + a + a + v + a + a + a
h4 = h + v + a + v + a + a + v + a + a + a + v + a + a + a + a
Or...
h1 = h + v + a
h2 = h + 2v + 3a
h3 = h + 3v + 6a
h4 = h + 4v + 10a
v component is linear
a component follows (n² + n)/2
So height after the nth time step is:
h(n) = h + nv + (n² + n)/2 * a
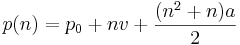
where
- p(n) is the position at the nth time step
- p0 is the starting position (0th time step)
- v is the starting velocity per time step
- a is the acceleration due to gravity per time step
I have seen a few people wondering why their trajectory prediction isn't quite giving them the result they were expecting, and I think mostly it's due to overlooking the very important point that everything in Box2D takes discrete movements between time steps. You cannot use a formula based on seconds, and plugin a value like 2.62 seconds to get an accurate value that will match how the Box2D body will advance along its projectile parabola.
However you could note that 2.62 seconds is 157 time steps (at 60fps) and use a formula like the one above to reproduce the same calculation that Box2D will actually carry out. It may not be obvious at first, but the reason that using seconds is unreliable is because the rate of acceleration per time step is different depending on how many time steps per second are used.
As an example, suppose you have an object at height 0, and you let it drop under a gravity of -10m/s/s for one second. No matter what time step you choose the velocity after one second will be -10m/s because this is what gravity is defined as, but the resulting position will be different depending on how many position and velocity updates were allowed during that one second time span:
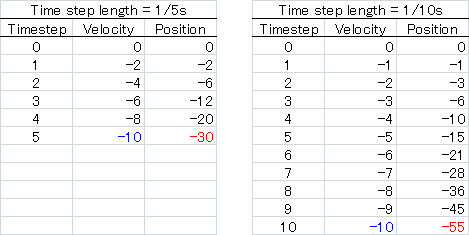On the left, the time step is much larger than on the right, so less steps are allowed per second
to reach the required -10m/s, which results in less distance covered overall. Anyway, just remember to be wary
of using seconds and we'll be fine.Drawing a projected trajectory
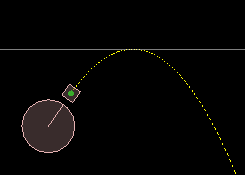
Most people coming to this page will be looking to make a visual indicator to show where a launched projectile will travel, so let's do that right away, then we can get to some trickier things after that. This is quite simple - we put the formula above into a function to make it a little more convenient:
1 2 3 4 5 6 7 8 9 | b2Vec2 getTrajectoryPoint( b2Vec2& startingPosition, b2Vec2& startingVelocity, float n ) { //velocity and gravity are given per second but we want time step values here float t = 1 / 60.0f; // seconds per time step (at 60fps) b2Vec2 stepVelocity = t * startingVelocity; // m/s b2Vec2 stepGravity = t * t * m_world->GetGravity(); // m/s/s return startingPosition + n * stepVelocity + 0.5f * (n*n+n) * stepGravity; } |
1 2 3 4 5 6 7 | glColor3f(1,1,0); glBegin(GL_LINES); for (int i = 0; i < 180; i++) { // three seconds at 60fps b2Vec2 trajectoryPosition = getTrajectoryPoint( startingPosition, startingVelocity, i ); glVertex2f(trajectoryPosition.x, trajectoryPosition.y ); } glEnd(); |
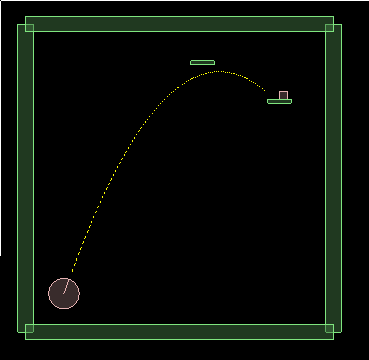To satisfy yourself that we've got the exact locations correct for the prediction,
pause the simulation and zoom in to check that the center of the box (green dot) is right on
the end of one of the yellow dashed lines at every step.
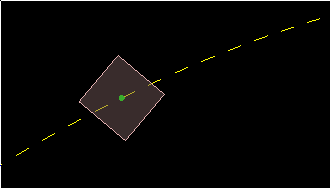In a real application you would probably only need to draw every nth position, instead
of drawing every position like in the example above. The plugin formula is handy for this
because we can just calculate the points for any time in the future we want instead of
needing to run through the whole simulation in sequence to find them.
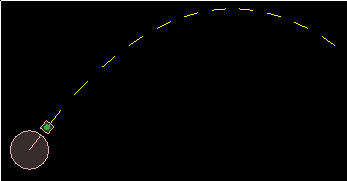Now how about some of those other questions that we were talking about...What will it hit?
As mentioned already, if there are other dynamic bodies moving around in the world, there is no way to correctly know what the projectile will hit without running the full simulation for the whole world. However in many cases it may just be good enough to show the user the first point that the trajectory would intersect something in the current state of the world.
This is pretty simple to accomplish by adding a raycast check to the loop which draws the projected trajectory. All you need to do is cast a ray between successive points along the trajectory until something is hit, and then stop drawing. Raycasting has been covered in other topics so I will direct you there for the details, or you can check out the source code at the end of this topic.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | TrajectoryRayCastClosestCallback raycastCallback; b2Vec2 lastTP = startingPosition; glBegin(GL_LINES); for (int i = 0; i < 180; i++) { b2Vec2 trajectoryPosition = getTrajectoryPoint( startingPosition, startingVelocity, i ); if ( i > 0 ) { //avoid degenerate raycast where start and end point are the same m_world->RayCast(&raycastCallback, lastTP, trajectoryPosition); if ( raycastCallback.m_hit ) { glVertex2f(raycastCallback.m_point.x, raycastCallback.m_point.y ); break; } } glVertex2f ( trajectoryPosition.x, trajectoryPosition.y ); lastTP = trajectoryPosition; } glEnd(); |
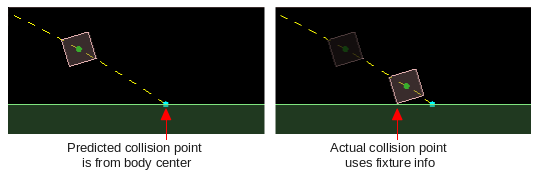
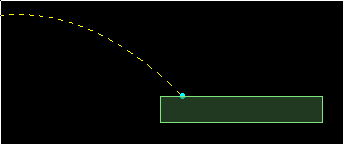One thing to keep in mind if you do this, is that the intersection point is only calculated
from the single-line path of the trajectory, which in this case is the center of the body
in motion. The actual first impact point between the body and the thing it hits will depend
on what fixtures the body has and how they are positioned.
Nevertheless, in many situations this would be enough to show the user a second trajectory
calculated from how the body would bounce. For example if the projectile is a circle and the thing
it hits is static, then the direction it will bounce off can be found with reasonable accuracy.How high will it go?
There are two related things we can look at here. One is finding out how high a projectile will get at its highest point, given a certain starting velocity - this is very similar to what we just did above. But probably the more common question people have is the opposite - how fast should I launch it so that it reaches a specific height?
These can both be answered by noting that when the projectile reaches its highest point, the velocity will be zero for a brief moment before it comes back down. If we could find out what the time step was at that time, we could use the original formula above to get the height.
The velocity part of projectile motion can be shown to be: (Click here for the long story.)
Velocity measured as distance moved per timestep
Acceleration measured as change in velocity per timestep
v = starting velocity
a = acceleration (gravity, constant)
Velocity changes by constant acceleration every time step
Velocity
v0 = v + a <- engine applies gravity before moving!
v1 = v0 + a
v2 = v1 + a
v3 = v2 + a
v4 = v3 + a
Expanded velocity
v0 = v + a
v1 = v + a + a
v2 = v + a + a + a
v3 = v + a + a + a + a
So velocity after the nth time step is:
v(n) = v + (n + 1) * a
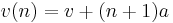where
- v(n) is the velocity at the nth time step
- v is the starting velocity per time step
- a is the acceleration due to gravity per time step
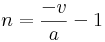This will give us the number of time steps until maximum height is reached, then we can
use that in the first formula, like this:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | float getMaxHeight( b2Vec2& startingPosition, b2Vec2& startingVelocity ) { //if the projectile is already heading down, this is as high as it will get if ( startingVelocity.y < 0 ) return startingPosition.y; //velocity and gravity are given per second but we want time step values here float t = 1 / 60.0f; b2Vec2 stepVelocity = t * startingVelocity; // m/s b2Vec2 stepGravity = t * t * m_world->GetGravity(); // m/s/s //find n when velocity is zero float n = -stepVelocity.y / stepGravity.y - 1; //plug n into position formula, using only vertical components return startingPosition.y + n * stepVelocity.y + 0.5f * (n*n+n) * stepGravity.y; } |
How fast should it be launched to reach a desired height?
From the previous section, we know the maximum height is reached when the velocity gets to zero and the object starts to fall down again, and we have a way to know how many time steps that will take for a certain launch velocity. But for this question we don't really care how long it takes to get to the maximum height, we care about the the initial velocity.
So taking the two equations from the previous section and substituting the 'timesteps to reach max height' expression into the original position formula, we can express the maximum height in terms of a and v only: (here I've ignored the initial position for clarity)
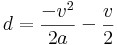where
- d is the vertical movement made before reaching the maximum height
- v is the starting velocity per time step
- a is the acceleration due to gravity per time step
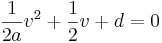Here is an example of how this could be done:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | float calculateVerticalVelocityForHeight( float desiredHeight ) { if ( desiredHeight <= 0 ) return 0; //wanna go down? just let it drop //gravity is given per second but we want time step values here float t = 1 / 60.0f; b2Vec2 stepGravity = t * t * m_world->GetGravity(); // m/s/s //quadratic equation setup (ax² + bx + c = 0) float a = 0.5f / stepGravity.y; float b = 0.5f; float c = desiredHeight; //check both possible solutions float quadraticSolution1 = ( -b - b2Sqrt( b*b - 4*a*c ) ) / (2*a); float quadraticSolution2 = ( -b + b2Sqrt( b*b - 4*a*c ) ) / (2*a); //use the one which is positive float v = quadraticSolution1; if ( v < 0 ) v = quadraticSolution2; //convert answer back to seconds return v * 60.0f; } |
The goal of this setup of course is to make the ball land on the tee and stay there, and if the horizontal velocity is not too large, the calculations we have looked at in this topic actually do a reasonable job of it. Because the projected trajectory only considers the center of the ball, it can hit the underside of the tee as it comes up, so there is a limited range in which the ball can land correctly with this simple technique. Anyway, you can check it out for yourself below.
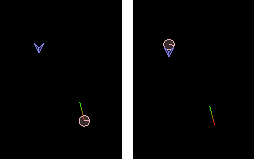Update:About the demo mentioned above where a ball is launched to land on the v-shaped target, the example code sets the target point to be exactly at the apex of the trajectory. The function calculateVerticalVelocityForHeight is used to find the vertical component of the launch speed, and the time taken to arrive at the maximum height is then calculated using the n = -v/a-1 formula above (see the 'getTimeToTop' function in the source code). Once we know how long the vertical part of the trajectory will take, we can set the horizontal component of the launch velocity so that the body will cover the horizontal distance to the target in the same time. You could think of this as the left half of the trajectory parabola below - eg. the h1 part of this diagram:
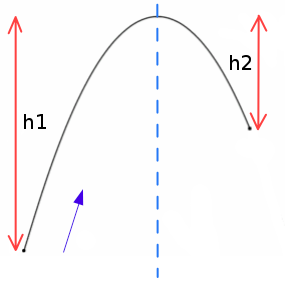If you want to calculate a trajectory that goes up and then down again to arrive at a target point, you
can repeat this process for each side of the parabola. First, you need to decide
what the maximum height should be at the apex. Then you can do calculateVerticalVelocityForHeight for each
side, from which you can find the time required for each side. Adding these times together will give you the
total time taken for the vertical component of the trajectory to reach the target, from which you can set
the horizontal component of the launch velocity as before. (If the target point is below the starting point
and you don't want the body to go up at all, you only need to consider the falling half of the parabola.)Source code
Here is the source code for those who would like to try it out for themselves. This is a 'test' for the testbed, based on Box2D v2.2.2.
ah... the functions are hardcoded to use 60fps time steps, so if you change the 'Hertz' setting on the testbed the calculations will be incorrect.
Testbed test: iforce2d_Trajectories.h
Linux binary
Windows binary
YouTube video