Forces and impulses

Box2D C++ tutorials - Forces and impulses

Last edited: July 14 2013

Chinese version -> 中文

To move things around, you'll need to apply forces or impulses to a body. Forces act gradually over time to change the velocity of a body while impulses can change a body's velocity immediately. As an example, imagine you have a broken down car and you want to move it. You could use a force by slowly driving another car up next to it until their bumpers touched and then push it, causing it to accelerate over time. Or you could use an impulse by driving the other car into it at full speed. Both methods have their place depending on what you are trying to simulate.

You can also 'warp' a body instantaneously by simply setting its location. This can be handy for games where you need a teleport feature, but bear in mind that this is not realistic physics! The whole point of a physics simulator like Box2D is to make things look real, and to this end I would recommend using forces and impulses to move bodies as much as you can. Sometimes it might seem tricky to think of a way to do this, but in the real world everything happens via forces or impulses, so unless you are creating a feature which is obviously not real-world (teleport etc), keep thinking. It may end up giving you less problems down the line.

Angular movement can also be controlled by forces and impulses, with the same gradual/immediate characteristics as their linear versions. Angular force is called torque. Think of this as a twisting strength, like when you twist the cap off a bottle - the bottle doesn't go anywhere, but you are still applying a force (torque) to it.

In this topic, we'll make three bodies and try using each one of the above-mentioned methods to move and twist them. Let's set up a scene similar to the one in the fixtures topic, but with all the shapes the same.

  //class member variable to keep track of three bodies
  b2Body* bodies[3];
  
  FooTest() {
    //body definition
    b2BodyDef myBodyDef;
    myBodyDef.type = b2_dynamicBody;
    
    //shape definition
    b2PolygonShape polygonShape;
    polygonShape.SetAsBox(1, 1); //a 2x2 rectangle
  
    //fixture definition
    b2FixtureDef myFixtureDef;
    myFixtureDef.shape = &polygonShape;
    myFixtureDef.density = 1;
    
    //create identical bodies in different positions
    for (int i = 0; i < 3; i++) {
      myBodyDef.position.Set(-10+i*10, 20);
      bodies[i] = m_world->CreateBody(&myBodyDef);
      bodies[i]->CreateFixture(&myFixtureDef);
    }
    
    //a static floor to drop things on
    myBodyDef.type = b2_staticBody;
    myBodyDef.position.Set(0, 0);
    polygonShape.SetAsEdge( b2Vec2(-15,0), b2Vec2(15,0) );
    m_world->CreateBody(&myBodyDef)->CreateFixture(&myFixtureDef);
  }

Linear movement

We need some way of affecting these bodies without using the mouse. Now would be a good time to check out the keyboard input feature of the testbed. Override the Keyboard function of the Test class to use a different method for each body:

  void Keyboard(unsigned char key)
  {
    switch (key)
    {
      case 'q':
        //apply gradual force upwards
        bodies[0]->ApplyForce( b2Vec2(0,50), bodies[0]->GetWorldCenter() );
        break;
      case 'w':
        //apply immediate force upwards
        bodies[1]->ApplyLinearImpulse( b2Vec2(0,50), bodies[1]->GetWorldCenter() );
        break;
      case 'e':
        //teleport or 'warp' to new location
        bodies[2]->SetTransform( b2Vec2(10,20), 0 );
        break;
      default:
        //run default behaviour
        Test::Keyboard(key);
    }
  }

The SetTransform function we covered in the bodies topic. The ApplyForce and ApplyLinearImpulse functions take two parameters, the first is what direction the force should be, in this case straight up. The second parameter is what point on the body should be pushed on - we'll get to this soon.

Run the test and try pressing the q/w/e keys. The impulsed body should react as if it was suddenly hit by something. The teleported body moves instantly to the new location, but notice that it retains its linear and angular velocity. What's happening with the body we applied the force to? Well, this Keyboard function is only called when we press the key down, not every timestep. In the example of car-pushing analogy, this would be like pushing the car for a fraction of a second, and then stopping. Since a force works over time, what we really need is some way to turn the force on and off instead of just blipping it on for a brief moment. We could use a class member variable to keep track of whether the force is on, and use the q key to toggle it. Make the following changes to the class:

  //class member variable
  bool forceOn;
  
  //inside constructor
  forceOn = false;
  
  //modified case for q key in Keyboard() function
    case 'q':
      forceOn = !forceOn;//toggle bool value
      break;
  
  //inside Step() function
      if (forceOn)
        bodies[0]->ApplyForce( b2Vec2(0,50), bodies[0]->GetWorldCenter() );

Now the q key should turn the force on and off, and you can see the gradual effect of a force.

Hmm.... we applied the same magnitude (50) for both impulse and force, so why does the force seem to be weaker than the impulse? Well, remember that gravity is a force too. Try turning gravity off and the answer might become clear. The reason is that the force acts a little bit each timestep to move the body up, and then gravity acts to push it back down again, in a continual up down up down struggle. The impulse on the other hand, does all its work before gravity gets a chance to interfere. With gravity off, try turning the force on for about one second, then off. You will notice that after one second, the forced body has the same velocity as the impulsed body.

Now what about the last parameter of the apply force/impulse functions that we have ignored? So far we set this using the GetWorldCenter() of the body which will apply the force at the center of mass. As we can see, a force applied to the center of mass does not affect the rotation of the body. Imagine a CD on a friction-less flat surface, like an air-hockey table. If you put your finger in the hole in the middle of the CD and flick it across the table, it will not spin around as it moves. But if you do this with your finger anywhere else on the CD, it will spin around as it moves, and the further away from the middle your finger was, the more it will spin.

Let's offset the point at which we apply the force/impulse. Change the ApplyForce and ApplyLinearImpulse calls so that instead of using GetWorldCenter() to apply force at the center of mass, we'll apply it at the top right corner of the box:

  //before
  GetWorldCenter()
  
  //after
  GetWorldPoint( b2Vec2(1,1) )

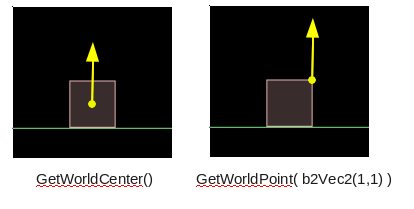This time, you should see these boxes rotate when acted upon. The function GetWorldPoint is used to convert a location relative to the body (body coordinates) into world coordinates, so that we keep applying the force at the corner of the box even after it has rotated around. Note that while the picture above shows a scenario which might be interpreted as 'picking the box up by its corner', the force being applied has nothing to do with the visible rectangle fixure - forces and impulses are applied to bodies, not their fixtures. The force could just as easily be applied at any old point, even in empty space where the body has no fixures.

Angular movement

Angular movement is controllable by using angular forces (torque) and angular impulses. These behave similar to their linear counterparts in that force is gradual and impulse is immediate. Let's add a couple of cases to the Keyboard() function to try them out. (Although there is a third case where the rotation can be set instanteously, we have already done that with SetTransform() above, so we'll skip that here.)

      case 'a':
        //apply gradual torque counter clockwise
        bodies[0]->ApplyTorque( 20 );
        break;
      case 's':
        //apply immediate spin counter clockwise
        bodies[1]->ApplyAngularImpulse( 20 );
        break;

Now use the a/s keys to see what happens. Once again you will see that to make the torque effective, you will need to add a class member variable to toggle the torque on/off so it can be applied constantly every time step:

  //class member variable
  bool torqueOn;
  
  //inside constructor
  torqueOn = false;
  
  //modified case for a key in Keyboard() function
    case 'a':
      torqueOn = !torqueOn;//toggle bool value
      break;
  
  //inside Step() function
      if (torqueOn)
        bodies[0]->ApplyTorque( 20 );

With gravity on, you'll see that even though we are only trying to 'twist' these boxes they still move around a bit, but that's only because they collide with the ground and act like square wheels. For a better illustration of what torque and angular impulse are doing, turn gravity off. In a zero-gravity scene, now we can see why only one parameter is necessary for angular force/impulse functions - since no linear movement is caused, the only thing we need to specify is which way the rotation should be. Unlike linear forces above there is never any offset possible because the rotation is always about the body's center of mass.

As with the linear forces, given the same magnitude parameter, ApplyTorque will take one second to gain as much rotational velocity as ApplyAngularImpulse does immediately.

Next: Custom gravity